Потік топологічних величин

Топологія - та область, що розвивається у багатьох наукових дисциплінах, навіть призвела до Нобелівської премії з фізики у 2016 році. Лейденський фізик Марчелло Кайо і його колеги тепер виявили існування топологічних струмів за аналогією з електричними струмами.
Їх дослідження опубліковано в Nature Physics 14 січня, повідомляють в Лейденському університеті.
Люди приписують властивості об′єктам, такі як колір, температура і фаза - газоподібний це об′єкт, рідкий або твердий. Наприклад, конкретна точка на поверхні пончика коричнева, тверда і має кімнатну температуру. Топологічні властивості різні. Вони містять інформацію про весь об′єкт. Наприклад, пончик має одну дірку. Неможливо підрахувати кількість дірок, зосередившись на певній частині пончика. Вам потрібно розглянути його в цілому. Топологія виявилася важливою в багатьох наукових сферах. У 2016 році, наприклад, робота з топології була визнана Нобелівською премією з фізики.
Індекс Черна
Так званий індекс Черна є іншою, хоча й дуже абстрактною, топологічною величиною. Це особливий випадок у топології. Нещодавно було виявлено, що індекс Черна має щільність, що називається маркером Черна. Це дає інформацію про топологію всієї системи, навіть якщо просто подивитись на локальний рівень. Суцільна лінія на малюнку внизу показує просторовий розподіл маркера Черна, де кожна локальна точка має свою власну величину. (Зауважте, що цей графік не має сенсу для глобальної властивості, подібної до кількості дірок в об′єкті.) Однак, локальні точки повинні дотримуватися одного правила на глобальному рівні: середнє значення всіх локальних значень завжди повинно дорівнювати нулю.
Топологічний струм
Лейденський фізик Марчелло Кайо разом з командою вчених зі Сполученого Королівства виявив, що якщо ви збурюєте систему, то локальні значення Черна будуть розподілятися, переходячи від кордонів до внутрішньої частини системи. Навпаки, глобальні топологічні властивості стійкі до збурень - кількість отворів у пончику змінюється тільки після великого укусу. На малюнку знизу збурення призводить до зміни форми графіка, аби продовжувати відповідати вимозі, що його інтеграл дорівнює нулю. Кайо і його колеги виявили, що це не відбувається миттєво, тому через систему має проходити маркер Черна. Це являє собою топологічний струм, по аналогії із звичайним електричним струмом.
Нові пристрої
Кайо каже: "У далекому майбутньому це може дозволити розробляти нові пристрої на основі топологічних струмів, окрім електричних струмів. Є багато місць для дослідження в цьому напрямку. Чи є інші шляхи для створення цього струму? Чи можемо ми керувати ними? Там багато цікавих можливостей".
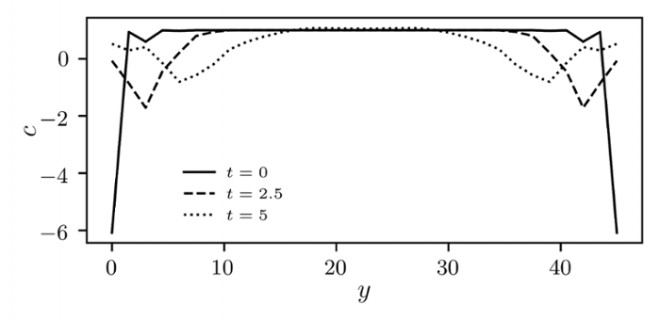
Три графіки для просторового розподілу (y) маркера Черна (c) в різний час. Суцільна лінія показує початковий стан, коли на краях має місце невелике збурення. Дві пунктирні лінії показують розподіл маркера Черна через деякий час. Зрозуміло, що збурення тече (не миттєво) до середини. Це означає, що ми розглядаємо топологічний струм.
Останні новини
| 07:24, 8 липня 2025 р. 8-13 липня в Києві проходять продуктові ярмарки | ||
| 18:31, 7 липня 2025 р. В поліції назвали причину потужних вибухів в Березині біля Жит... | ||
| 03:36, 10 липня 2025 р. Країна-терорист атакує Київ шахедами й балістичними ракетами | ||
| 08:36, 7 липня 2025 р. Розпочалася 1230-а доба повномасштабного російського вторгнення | ||
| 01:08, 7 липня 2025 р. З МКС сфотографували рідкісний червоний спрайт над хмарами | ||


